Utformning avfotoniskintegrerad krets
Fotoniska integrerade kretsar(PIC) utformas ofta med hjälp av matematiska skript på grund av vikten av väglängd i interferometrar eller andra tillämpningar som är känsliga för väglängd.BILDtillverkas genom att applicera flera lager (vanligtvis 10 till 30) på en wafer, som består av många polygonala former, ofta representerade i GDSII-format. Innan filen skickas till fotomasktillverkaren är det starkt önskvärt att kunna simulera PIC:n för att verifiera designens korrekthet. Simuleringen är uppdelad i flera nivåer: den lägsta nivån är den tredimensionella elektromagnetiska (EM) simuleringen, där simuleringen utförs på subvåglängdsnivå, även om interaktionerna mellan atomer i materialet hanteras i makroskopisk skala. Typiska metoder inkluderar tredimensionell finita-differens-tidsdomän (3D FDTD) och egenmodsexpansion (EME). Dessa metoder är de mest exakta, men är opraktiska under hela PIC-simuleringstiden. Nästa nivå är 2,5-dimensionell EM-simulering, såsom finita-differens-strålutbredning (FD-BPM). Dessa metoder är mycket snabbare, men offrar viss noggrannhet och kan bara hantera paraxiell utbredning och kan inte användas för att simulera resonatorer, till exempel. Nästa nivå är 2D EM-simulering, såsom 2D FDTD och 2D BPM. Dessa är också snabbare, men har begränsad funktionalitet, till exempel kan de inte simulera polarisationsrotatorer. En ytterligare nivå är transmissions- och/eller spridningsmatrissimulering. Varje huvudkomponent reduceras till en komponent med ingång och utgång, och den anslutna vågledaren reduceras till ett fasförskjutnings- och dämpningselement. Dessa simuleringar är extremt snabba. Utsignalen erhålls genom att multiplicera transmissionsmatrisen med ingångssignalen. Spridningsmatrisen (vars element kallas S-parametrar) multiplicerar ingångs- och utsignalerna på ena sidan för att hitta ingångs- och utsignalerna på den andra sidan av komponenten. I grund och botten innehåller spridningsmatrisen reflektionen inuti elementet. Spridningsmatrisen är vanligtvis dubbelt så stor som transmissionsmatrisen i varje dimension. Sammanfattningsvis, från 3D EM till transmissions-/spridningsmatrissimulering, presenterar varje simuleringslager en avvägning mellan hastighet och noggrannhet, och konstruktörer väljer rätt simuleringsnivå för sina specifika behov för att optimera designvalideringsprocessen.
Att förlita sig på elektromagnetisk simulering av vissa element och använda en spridnings-/överföringsmatris för att simulera hela PIC:n garanterar dock inte en helt korrekt design framför flödesplattan. Till exempel kommer felberäknade väglängder, multimodvågledare som inte effektivt undertrycker högordningens moder, eller två vågledare som är för nära varandra vilket leder till oväntade kopplingsproblem sannolikt att gå oupptäckta under simuleringen. Därför, även om avancerade simuleringsverktyg ger kraftfulla designvalideringsmöjligheter, kräver det fortfarande en hög grad av vaksamhet och noggrann inspektion av konstruktören, i kombination med praktisk erfarenhet och teknisk kunskap, för att säkerställa designens noggrannhet och tillförlitlighet och minska risken för flödesschemat.
En teknik som kallas gles FDTD gör det möjligt att utföra 3D- och 2D FDTD-simuleringar direkt på en komplett PIC-design för att validera designen. Även om det är svårt för något elektromagnetiskt simuleringsverktyg att simulera en mycket storskalig PIC, kan den gles FDTD simulera ett ganska stort lokalt område. I traditionell 3D FDTD börjar simuleringen med att initiera de sex komponenterna i det elektromagnetiska fältet inom en specifik kvantiserad volym. Allt eftersom tiden går beräknas den nya fältkomponenten i volymen, och så vidare. Varje steg kräver mycket beräkning, så det tar lång tid. I gles 3D FDTD, istället för att beräkna vid varje steg vid varje punkt i volymen, upprätthålls en lista över fältkomponenter som teoretiskt kan motsvara en godtyckligt stor volym och beräknas endast för dessa komponenter. Vid varje tidssteg läggs punkter intill fältkomponenter till, medan fältkomponenter under ett visst effekttröskelvärde utelämnas. För vissa strukturer kan denna beräkning vara flera storleksordningar snabbare än traditionell 3D FDTD. Glesa FDTDS fungerar dock inte bra vid hantering av dispersiva strukturer eftersom detta tidsfält sprider sig för mycket, vilket resulterar i listor som är för långa och svåra att hantera. Figur 1 visar ett exempel på en skärmdump av en 3D FDTD-simulering som liknar en polarisationsstråldelare (PBS).
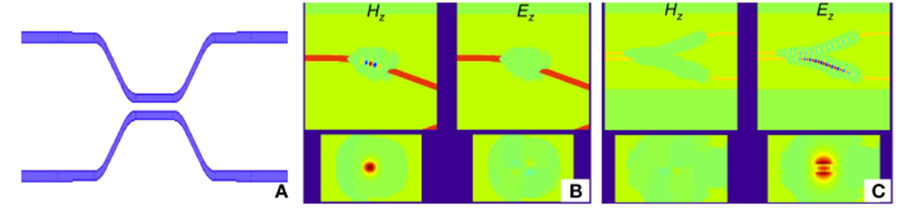
Figur 1: Simuleringsresultat från 3D gles FDTD. (A) är en toppvy av strukturen som simuleras, vilket är en riktningskopplare. (B) Visar en skärmdump av en simulering med kvasi-TE-excitation. De två diagrammen ovan visar toppvyn av kvasi-TE- och kvasi-TM-signalerna, och de två diagrammen nedan visar motsvarande tvärsnittsvy. (C) Visar en skärmdump av en simulering med kvasi-TM-excitation.
Publiceringstid: 23 juli 2024





